Ewa Damek
Uniwersytet Wrocławski

Wyobraźmy sobie, że mamy dwuwymiarowy proces stochastyczny (X_t , Y_t) z czasem dyskretnym tzn. opisujący zachowanie się dwóch instrumentów finansowych. Załóżmy,  że każdy z nich spełnia afiniczne równanie stochastyczne

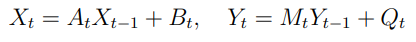
i z założeń wynika, że ogony X_t i Y_t malej wielomianowo tzn.

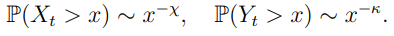
Co możemy powiedzieć o

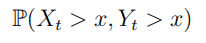
i jak w ogóle dobrze sformułować problem? Tzn. jak opisać wzajemną zależność X_t i Y_t?

Ostatnio udało mi się udowodnić twierdzenie, które daje dobrą odpowiedź na to pytanie dla n procesów, a w szczególności takich, które stosowano do opisu instrumentów finansowych. Przedstawimy przykłady i sformułujemy twierdzenie.

Wykład odbędzie się 8 grudnia 2021 o godzinie 17.30 przy użyciu komunikatora Zoom.